13.3. Conditioning on a collider

For our final mind-bending challenge to inference (these are heavy ones in this chapter, aren’t they?) we turn to a lesser-known, rather sneaky, but quite potentially sinister third variable problem: conditioning on a collider. To begin, let’s briefly recap our earlier third variable problem, confounders.

Confounders vs. colliders

Confounders

As we know, a confounder is a third variable that exerts influence on both \(x\) and \(y\). Omitting a collider from our analysis can distort the association between \(x\) and \(y\) in our results. It often can make it look like there is an association between two variables, when in fact there is not – rather, some missing third variable (a confounder) is driving the pattern we observe.

We’ve seen lots of examples of these, some of them of course rather silly and obvious, such as that shoe size is positively associated with spelling ability. The inference is faulty in this case because we’re leaving out age, which influences both shoe size and spelling ability.

Of course, confounders are often harder to detect than the above example. For example, suppose a study finds that people who go to yoga class regularly have higher self-reported happiness. A reasonably conclusion could be that more yoga will give rise to more happiness (and as someone who goes to yoga, I obviously have a stake in this conclusion), but it’s also possibly the case that we’re missing an underlying third variable, such as money, free time, or a commitment to personal health – all of which we could also imagine both being positively associated with going to yoga and having higher self-reported happiness. Of course, this isn’t the end of the road, but rather the beginning – we can now investigate these other variables and keep refining our understanding of how they all fit together. But recognizing the possibility of a confounder in the first place is a crucial step.

Colliders

A collider is a third variable on which both \(x\) and \(y\) exert influence. Including a collider in our analysis can distort the association between \(x\) and \(y\) in our results. It can often make it look like there is no association between two variables when there is one, or that there is, e.g., a negative association when there is a positive one. Including a collider can take a variety of forms, such as including it as a variable or control in our model, or selecting observations on the basis of that variable – we call this conditioning on a collider.

In the case of our yoga and happiness example above, we already saw some challenges arise when we failed to include a confounder, such as income, and observed a (possibly distorted) positive association between yoga and happiness. Suppose we wanted to explore the possibility of a confounder of income, and we’ll do so first by investigating whether income might be exerting an influence on how much we do yoga. So, we ask attendees at the next wellness retreat that we also happen to attend (hypothetically speaking) to tell us how often they go to yoga as well as how much money they make in a year (assume further that everyone is somehow magically open to telling us this information; I mean, I think we all know nothing opens a chakra like radical honesty, so it should be fine. Ommm!).

After we collect our results on yoga frequency and annual income, we plot our results in a simple scatterplot and calculate a Pearson’s correlation coefficient, and are shocked to find no association between yoga and income. “Downward doggone it!” we might exclaim, because we’re so surprised that perhaps income is not a confounder after all, and now we need to rethink our whole study, and never mind worldview on yoga, income inequality, and late stage capitalism.

But we may in fact be observing a lack of association when in fact there is one in reality, and this is because we are conditioning on a collider. As you may have notice, we specified in this example that our observations are all of attendees at a wellness retreat. It’s plausible that our \(x\) and \(y\) variables both influence attendance at a wellness retreat. Specifically, being more interested in yoga might make you more likely to attend a wellness retreat. And, having a higher income might make you more likely to attend a wellness retreat.

Where things get even more wild is that not only are our subjects in our dataset for reasons related to both variables, but it’s it’s also highly plausible that people who ultimately show up at this wellness retreat are doing so in such a way that it exactly offsets the true, underlying association between \(x\) and \(y\). To see this, consider the three types of people who likely attend a wellness retreat:

• People who have both a medium interest in yoga and enough disposable income that they can afford the retreat

• People who have a low interest in yoga but a high income but are trying to kick start a habit or they read about it on Goop (congratulations to us for surely being the first data science textbook to ever reference Goop; also, we are sorry)

• People who have a high interest in yoga and a low income, but love yoga so much they scrape together their funds to go as a special treat to themselves

This means that within the population we are studying, it will appear as though there is no association between yoga and income even though in reality, there is. (Note: this is a hypothetical example for illustrative purposes only; please do not come at us, Big Yoga.)

The image below describes the two scenarios of a confounder and collider in our fascinating yoga study, and how each third variable relates to our \(x\) and \(y\)

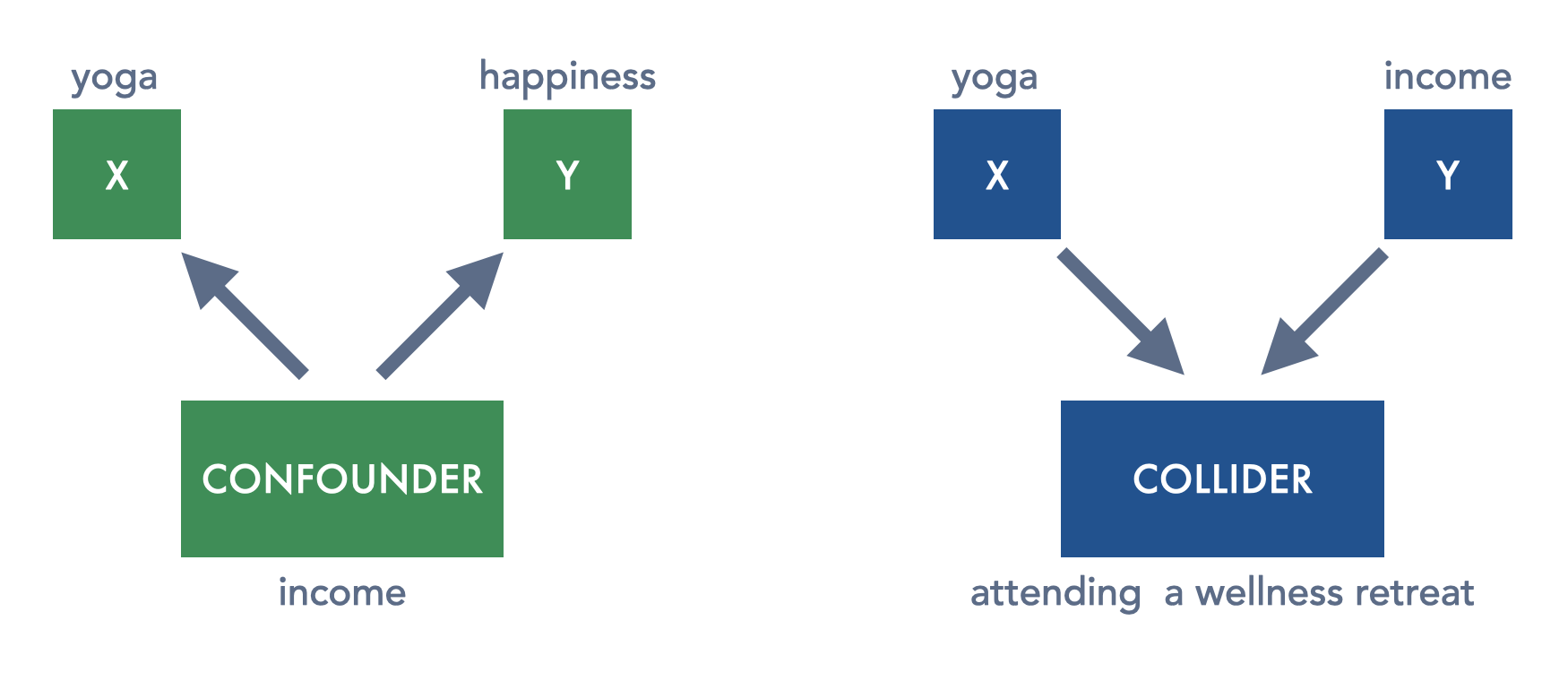
Fig. 13.2 Confounders influence both \(x\) and \(y\). Colliders are influenced by both \(x\) and \(y\)

Examples in the wild

Conditioning on a collider is not just a problem that plagues those of us looking for some inner peace. Here are a few examples of conditioning on a collider in the “real world”.

Height vs. salary in the NBA

A surprising finding from analyses of data on players’ heights versus their salaries is that there is little to no correlation between the two. This seems unexpected, because generally height is considered to be an advantage in basketball, and thus it’s reasonable to expect that their salaries, which are likely a proxy for skills, or value on the team, would thus be positively associated with height. This caused everyone to question everything they knew about basketball for awhile, until it came to bear that we had been conditioning on a collider, in this case, being in the NBA.

Consider how players are chosen for the NBA: they might be very tall and probably at least skilled enough to get in, but their height might be a serious advantage on its own. On the other hand, NBA players who are short were probably chosen because they are so skilled or have a particular kind of skill that the team needs, and thus are also valuable. We will end up with a low or zero correlation between height and salary in our analysis because players are chosen for the NBA in a way that exactly offsets the association between height and value for the team.

SATs vs. GPA in college

A finding that influenced the conversation around standardized testing and college admissions is a well-known one that SAT scores do not tend to do a good job of predicting success in college, perhaps measured as GPA (though of course we could consider others). As with the NBA example, it’s worth thinking about how students are selected for admission into college: they probably have high SAT scores, or if they don’t, they have some other quality (high school grades, extracurriculars, etc.) that makes them a strong candidate despite their lower SAT scores. Thus, we have conditioned on the collider of being in college.

Age and Covid seriousness

A recent example of conditioning on a collider that had a serious impact on policy and public perceptions of the pandemic came from early data on age and how serious a Covid infection might be. One of the earliest observations of Covid was that it seemed to be particularly dangerous for older people. Yet, some of the data that was coming our of hospitals indicated a lack of association between age and the seriousness of Covid infections. It was some time before we had enough other information, and enough people had time to work on the problem, that researchers realized that because early on the vast majority of data on Covid came from hospitals, that meant we were conditioning on a collider, because both age and having serious Covid influence whether or not someone is hospitalized. In particular, young people with particularly bad Covid were in these datasets specifically because they were hospitalized.

What to do about this?

In the three examples above from the NBA, SATs, and Covid, we might say, ok, one way around this is to expand our dataset so that we’re not conditioning on a collider. In some cases this is feasible – for example, researching the relationship between height and salary among broader populations reveals a positive association (which is striking for its own reasons!). But this is not always practical. In the case of Covid, early on we didn’t really have data from anywhere but hospitals, nor was there the bandwidth to collect it any more than we already were. And in the case of college students, it doesn’t really conceptually even work to consider a different population – if we want to understand whether SAT scores predict success in college, it makes sense that we are studying college students. Further, if we imagined expanding to non-college students, which perhaps in principle we could, we would be limited to people who took the SAT, but then did not go to college, which on the one hand would likely be a relatively small population, and on the other introduces its own additional complications, because there are likely reasons someone bothered to take the SAT but then did not go to college that are also related to exactly what we are trying to study.

Some options for addressing conditioning on a collider include:

1. Awareness

Conditioning on a collider is not nearly as well known as the problem of confounders or even other missing variables, yet it can influence our results. This means many empirical studies are likely out there today making claims about associations that are distored. Knowing about the potential for this problem can help us all start looking for these issues in our areas of study.

2. Detection

Figuring out if a collider might be at work in our research is not easy, nor are we guaranteed to ever really figure it out (just as various debates around confounders continue to exist, though we hope they become clearer over time), but one way to work out in your own or a study you read whether there might be a collider is to construct Directed Acyclic Graphs, or DAGs, which are diagrams of the causal relationships between the variables in our study. This may seem simple, but visualizing how your variables might influence one another not only helps clarify for you what might be going on, but also helps you communicate to others what you suspect may be afoot, as well as invite other ideas. In fact, we call it a collider because the arrows from our \(x\) and \(y\) collide with that variable in our DAGs!

Fig. 13.3 Directed Acyclic Graphs (DAGs)

3. Research design

Once we know to look for and detect what we suspect is likely a collider, we can adjust our research design to address it. If it happens that we’ve simply included a collider variable as a control variable in, say, a linear regression model, we can start by removing that variable. In other cases, such as in some of the examples above, we can expand our data collection methods such that we are not conditioning on a collider (e.g., ask regular humans about yoga and money, though ensuring a random sample that’s entirely orthogonal to those variables is not necessarily a trivial task). In other cases, we might need a more imaginative research design, or we are simply stuck with what we have and adjust our inferences (and how we communicate our results) accordingly.

Conditioning on a collider vs. selection on the dependent variable

Because conditioning on a collider can happen as a result of the fact that the data are selected into the study on the basis of their status with respect to a particular variable, a common question from students over the years has been what the difference is between conditioning on a collider and selecting on the DV. This is an important distinction.

The difference comes down to which variable we are selecting on. If we want to study the relationship between \(x\) and \(y\) and we select on \(y\), we are selecing on the DV. If we want to study the relationship between \(x\) and \(y\) and we select on some third variable \(z\) which is influenced by both \(x\) and \(y\), then we are conditioning on a collider.

The great collide

Conditioning on a collider is a tricky beast; it’s not widely known, it can be tricky to get one’s head around, it can be difficult to detect, and it can be difficult to do much about our analyses once we’ve detected them, or even if we suspect one might be afoot. As with all tricky problems, however, awareness is the first step, and we trust you will, at minimum, after having read this section, go out and regale your friends, family, and loved ones about this lesser known but impactful third variable problem. Later, you can remind them that you knew about it before it was cool.